Understanding GWAS

Understanding GWAS … or what is up with all those small odds ratios? The following is a gross oversimplification of GWAS studies and may include well meaning sarcasm.
What can Genome-Wide Association Studies (GWAS) tell us about disease? Why test over one million independent features of the genome and endure serious multiple testing abuse? The answer is pretty simple, for two very simple reasons. First, every candidate associated region of genes (a.k.a. the locus) broadens the scope of our knowledge about a disease. Secondly, all of those cumulatively small effects you observe, each giving a marginal increase in genetic risk, helps us better predict risk and refine diagnostic criteria. It’s said that GWAS is hypothesis free, but in reality the hypothesis is “a variant or set of variants in the genome might be doing some bad stuff, we need to find out more.”
On the most basic level, a GWAS is just a series of equations, each one looking at one genomic variant at a time. Let’s break this down in the setting of Parkinson’s Disease.
Parkinson’s disease (1 if yes, 0 if no) ~ β0 + β1variant + β2sex + β3age + β4PC1 + β5PC2
If you are familiar with statistics, your standard GWAS formula is just a simple multiple regression formula. This particular equation is testing if we can predict whether a person has Parkinson’s disease or not using the presence of a specific variant in that person’s genome. In addition to the tested variant, we include other factors such as sex, age, and principal components that explain individual level genetic ancestry.
Now let’s talk about odds ratios and betas. In the above equation, the ‘βn’ terms in front of the variables are coefficients. These tell us how much the estimated likelihood or ‘risk’ of Parkinson’s disease increases or decreases depending on the presence of that variable. In GWAS manuscripts, you will see these variant effect sizes reported as either beta values or odds ratios. Let’s look at an example for interpreting both. In the most recent and largest PD GWAS to date (Nalls 2019), one of the new variants found to be significantly associated with PD is the variant rs76116224 on chromosome 2. The beta value associated with this variant is 0.110. The odds ratio is 1.12 (confidence interval: 1.08–1.16). The beta value is the per unit increase or decrease in the outcome. So in this study:
- One copy of the rs76116224 variant has an estimated increased Parkinson’s disease risk of 0.110 * 1 = 0.110.
- Two copies of the rs76116224 variant have an estimated increased Parkinson’s disease risk of 0.110 * 2 = 0.220.
Odds ratios (OR) are the exponent of the beta coefficients, but are interpreted slightly differently. An OR of greater than 1 is associated with higher odds of the outcome, an OR of 1 means no association, and an OR of less than 1 is associated with lower odds of the outcome. So an OR of 1.12 means we will expect to see a 12% increase in the odds of having Parkinson’s disease for a one unit increase in variant copy.
Now that you have the equation down, you just have to calculate it for every variant in your data. So depending on how your data has been processed, just around 25,375,550 times! Luckily we have nice software to run all these equations for us.
Typically, each GWAS is done at a separate center on their own data, per ancestry and per individual cohort. However, the more people we include, the higher chances there are of detecting rare effect variants. To increase these numbers, each GWAS will be combined in a meta-analysis. Collaborative sites will agree ahead of time on how the disease or other outcome is defined, what code and compute infrastructure to use, and in some situations, even authorship order on resulting papers. Each study site usually agrees to basic quality control (QC) parameters for their study-level genotyping array data, as well as a consensus method of imputation (using the same reference panel to infer non-assayed genetic variants). The chosen quality control parameters must be performed before running your GWAS.
After QC is done and each individual GWAS is run, meta-analytic techniques from basic statistics are used to combine the GWAS summary statistics into a single aggregate results set per variant. From here, after some additional QC, you are able to start looking for variants with p-values < 5e-08 (this cut-off is typically chosen for GWAS to correct for multiple tests in the millions, but it may be better to be even more stringent). Variants that pass this significance threshold are considered to be significantly associated with the tested outcome, but it’s important to attempt to replicate these findings in additional datasets.
Variants discovered by GWAS give us targets to investigate and help increase our knowledge of disease. Every new target helps us build our ability to accurately predict a person’s risk of developing a certain outcome. These insights will be necessary as we move towards a precision medicine approach in treatment of disease. With GP2, we are committed to expanding this knowledge around Parkinson’s disease. Many of our GWAS processes are automated, and the code we use is public, transparent, and constantly growing. We are focused on diversity, so we deal in integrated analyses across global silos of data, analyzing as harmonized, united cohorts when possible, and meta-analyzing when appropriate.
A great amount of effort has been put into building uniform and clear workflows and code that we hope will be used by multiple researchers and institutions around the world. Our goal is to make GP2 the most transparent open science analytics project on the planet.
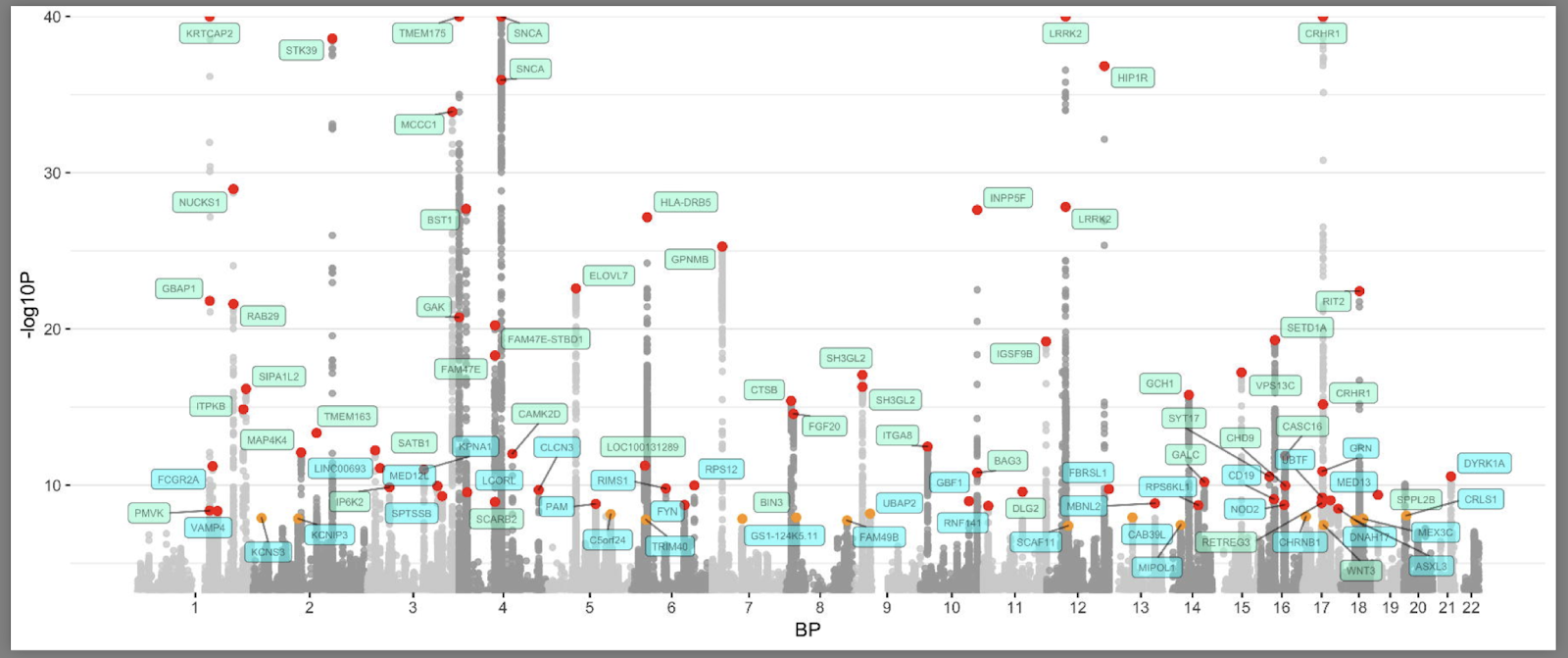
Here is what the current “Manhattan plot” (named after the towers in Manhattan) for Parkinson’s disease GWAS looks like (Nalls et al., 2019). You can find the code for this here.
You can find our code and pipelines at the GP2 GitHub, and look out for a follow-up blog post providing insights and tips for running your own GWAS.